Level of Measurement
Variables may be not only numeric but can also include qualitative attributes. Following Stevens  and Conover and Conover  , four types of scales (levels of measurement) can be distinguished: , four types of scales (levels of measurement) can be distinguished:
- Nominal scale: this scale is based on a set of qualitative attributes.
There is no criterion to order the items of a nominally scaled variable. Only the direct comparison ("is equal" and "is not equal") is possible and allowed. Examples: species, sex, treatment groups in experimental designs. Variables which exhibit only two categories are called dichotomous variables 1).
-
Ordinal scale: this scale refers to measurements that can be ordered in terms of "greater", "less" or "equal". Observations need not be equidistant. An ordinal scale allows to order the objects. The ordinal scale is therefore sometimes also called rank scale. Examples: percentile ranks, grades at school, ranks in a race, Mohs' scale of hardness (which exhibits unequal distances).
-
Interval scale: equally spaced units along the scale without a predefined zero point. Examples: temperature (in C, F, or R), water level of a river. Interval scaled data can be transformed by a linear transformation of the type y = x + d without losing their characters (thus interval scales remain interval scales, under certain circumstances even a ratio scale may be achieved).
-
Ratio scale: equally spaced units along the scale with a true zero point. Examples: temperature in K, weight, driving speed. Ratio scaled data can be transformed by the linear transformation y = k
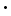 x+d without losing their character. This transformation is applied, for example, when converting meters to inches. x+d without losing their character. This transformation is applied, for example, when converting meters to inches.
It is true that for ratio scales a value two times greater corresponds to a property two times greater (100 km/h is twice as fast as 50 km/h). In contrast, this is not true for interval scales (the level of a river at 2.40 m is not twice as high as the level at 1.20 m, since the origin of the level scale has been set arbitrarily; a level of 0.0 m does not mean an empty river).
Please keep in mind that arithmatic operators are meaningful only for interval and ratio scales, multiplication and division are only applicable to ratio scales. In many fields of statistics (e.g. in sociology or psychology) ratio scales are only of limited importance, as most measurements and observation do not show a "natural" zero point. Practically speaking, almost all methods developed for interval scales may also applied to data which following a ratio scale. Interval scale and ratio scales are therefore summarized using the term metric scales or cardinal scales.
The following table gives a survey of the properties of the above mentioned scales together with a view examples:
| Type of Scale |
Possible Statements |
Allowed Operators |
Examples |
| nominal scale |
identity, countable |
=, 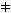 |
colors, phone numbers, feelings |
| ordinal scale |
identity, less than/greater than relations, countable |
=, 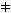 , <, > , <, > |
soccer league table, military ranks, energy efficiency classes |
| interval scale |
identity, less than/greater than relations, equality of differences |
=, 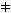 , <, >, +, - , <, >, +, - |
dates (years), temperature in Celsius, IQ scale |
| ratio scale |
identity, less than/greater than relations, equality of differences, equality of ratios, zero point |
=, 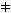 , <, >, +, -, *, / , <, >, +, -, *, / |
velocities, lengths, temperatur in Kelvin, age |
|


 Basic Concepts
Basic Concepts  Scale of Measurement
Scale of Measurement Basic Concepts
Basic Concepts  Scale of Measurement
Scale of Measurement

 x+d without losing their character. This transformation is applied, for example, when converting meters to inches.
x+d without losing their character. This transformation is applied, for example, when converting meters to inches.