Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more.

Home Bivariate Data Curve Fitting Curve Fitting by Splines
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter

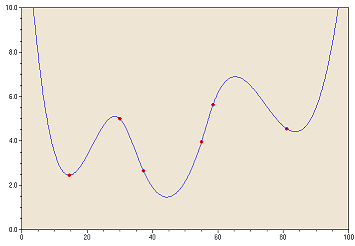
Curve Fitting by Splines

Cubic splines are a common class of functions which are used in many interpolation applications. The basic idea is to fit cubic polynomials between two neighboring data points while ensuring that certain additional conditions are fulfilled (smooth first and second derivative). Furthermore, the concept of splines can be extended to approximations as well, if we introduce a small extension which results in smoothed splines. A smoothed spline degenerates to a simple linear regression if the smoothing factor approaches its maximum.

Assume that we have n+1 data points [xi, yi] with i=0 to n, and x0 < x1 < .... < xn. Then the function S(x) is called a Cubic Spline if there exist n cubic polynomials si(x) having the coefficients ai,0, ai,1, ai,2, ai,3 that satisfy the following conditions:

  • S(x) = Sk(x) = ak,0 + ak,1(x-xk) + ak,2(x-xk)2 + ak,3(x-xk)3 for x [xk, xk+1] and k=0,1,2...n-1
  • The spline passes through each data point: S(xk) = yk for k=0,1, ... ,n
  • The spline forms a continuous function: Sk-1(xk) = Sk(xk) for k=1,2,....n-1
  • The spline forms a smooth function: S'k-1(xk) = S'k(xk) for k=1,2,....n-1
  • The second derivative is continuous: S"k-1(xk) = S"k(xk) for k=1,2,....n-1

Click on this image to experiment with spline interpolation.

Please note that there exists a unique cubic spline (called natural spline) with the boundary conditions S"(x0) = 0 and S"(xn) = 0. The natural spline is the curve obtained by forcing a flexible elastic rod through the points but letting the slope at the ends be free to equilibrate to the position that minimizes the oscillatory behavior of the curve.

Home Bivariate Data Curve Fitting Curve Fitting by Splines

Last Update: 2010-03-18