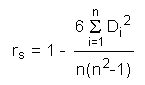Spearman's Rank Correlation

Calculating Pearson's correlation coefficient requires the two samples to be linearly related and the scale of measurement has to be at the interval level. In the case of non-linear relations, Pearson's correlation coefficient will lead to wrong results. A remedy to this situation may be the use of Spearman's rank correlation r_s (), which can be applied to ordinal data as well. The relation may be even non-linear as long as it is monotonic.

Basically, r_s differs from Pearson's correlation only in that the values are converted to ranks before computing the coefficient (the numerical equivalence is only true for untied data, in the case of tied data Pearson's and Spearman's coefficient will be slightly different).

When replacing the observation values with the rank numbers the equation of the correlation coefficient may be simplified, resulting in the following formula:

with D_i being the differences of the rank numbers. The equation is valid when n is greater than 4. In the case of tied observations one has to take the arithmetic average of the rank numbers associated with the ties.

Example:

Two persons taste 10 red Italian wines, grading them by an ordinal scale between 1 and 5. The results are as follows: Grades Grades Wine No. Person 1 Person 2 1 1 2 2 2 3 3 4 5 4 5 4 5 2 2 6 2 2 7 4 3 8 3 4 9 1 3 10 4 2 In order to calculate Spearman's rank correlation coefficient we first have to sort the grades for each person. The resulting rank numbers are averaged for tied observations: Grades Rank Rank Wine No. Person 1 (ties) 1 1 1 1.5 9 1 2 1.5 6 2 3 4 5 2 4 4 2 2 5 4 8 3 6 6 10 4 7 8 7 4 8 8 3 4 9 8 4 5 10 10 Grades Rank Rank Wine No. Person 2 (ties) 5 2 1 2.5 1 2 2 2.5 10 2 3 2.5 6 2 4 2.5 2 3 5 6 7 3 6 6 9 3 7 6 8 4 8 8.5 4 4 9 8.5 3 5 10 10 The final table of ranks includes the differences of the ranks as well as the squared differences: Wine No. Person 1 Rank Person 2 Rank Rank squared Difference Diff. 1 1 1.5 2 2.5 -1 1 2 2 4 3 6 -2 4 3 4 8 5 10 -2 4 4 5 10 4 8.5 1.5 2.25 5 2 4 2 2.5 1.5 2.25 6 2 4 2 2.5 1.5 2.25 7 4 8 3 6 2 4 8 3 6 4 8.5 -2.5 6.25 9 1 1.5 3 6 -4.5 20.25 10 4 8 2 2.5 5.5 30.25 ------------------------------------------------------------------------ sum 0.0 76.50 The sum of the squared differences is used to calculate Spearman's rank correlation coefficient as follows: rs = 1 - (6*76.5/(10*(100-1)) = 0.5364