| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Univariate Data Univariate Data  Measures of Location Measures of Location  Mean Mean  Confidence Interval of the Mean Confidence Interval of the Mean |
|||||
| See also: mean, t distribution | |||||
Confidence Interval of the MeanIf the mean is calculated from a sample, one wants to know the probability that the true mean lies within certain limits around the calculated mean. These limits are established by the confidence interval. The width of the confidence interval depends on the probability P that the true mean is found within the limits. The probability P is usually specified as α = 1-P; α is called the level of significance. The confidence interval of the mean is defined by  , ,with tn-1;1-α/2 being the critical value of the t distribution with n-1 degrees of freedom and a level of significance of 1-α/2.
The factor When reading publications one often finds the precision of measurements specified in different (and confusing) ways: some authors indicate the confidence interval as defined above, others specify the standard error only, and still others use the standard deviation of the sample to indicate the uncertainty of a measurement. In general, one should always specify the confidence interval (and its level of significance) together with the mean. The standard error overestimates the actual precision of the measurement (i.e. the standard error is alway narrower than the confidence interval) while the standard deviation of the sample underestimates it.
|
|||||
Home  Univariate Data Univariate Data  Measures of Location Measures of Location  Mean Mean  Confidence Interval of the Mean Confidence Interval of the Mean |
|||||


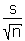 is called the standard error of the mean and can be regarded as some kind of standard deviation of the mean, because the mean of samples shows a variation which is controlled by the
is called the standard error of the mean and can be regarded as some kind of standard deviation of the mean, because the mean of samples shows a variation which is controlled by the