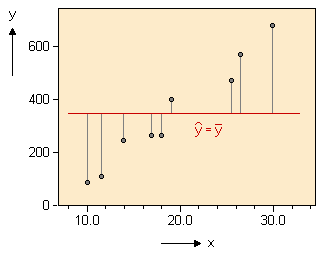
Regression - Coefficient of Determination

When calculating a regression model, we are interested in a measure of the usefulness of the model. There are several ways to do this, one of them being the coefficient of determination (also sometimes called goodness of fit). The concept behind this coefficient is to calculate the reduction of the error of prediction when the information provided by the x values is included in the calculation.

So we have to look at two cases:

(1) we assume that x does not contribute to the prediction of y:  the best guess for the predicted value of Y is the mean of all y values. The sum of squared errors is given as

(2) we include the information provided by x for the prediction of y: this means that the errors are reduced, since the regression line represents a best fit to the data. The sum of squared errors is then given as

The coefficient of determination is then the relative reduction of the error when the information in x is included to the model:

Thus the coefficient of determination specifies the amount of sample variation in y explained by x (or put it in another way: the coefficient of determination measures the variance which the two variables have in common). For simple linear regression the coefficient of determination is simply the square of the correlation coefficient between Y and .