| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Bivariate Daten Bivariate Daten  Glättung Glättung  Savitzky-Golay Filter Mathematische Details Savitzky-Golay Filter Mathematische Details |
|
| Siehe auch: Grundtypen von Filtern, Savitzky-Golay-Filter, Savitzky-Golay-Filter - Koeffizienten, Filter - Mathematischer Hintergrund | |
| Search the VIAS Library | Index | |
|
Savitzky-Golay Filter - Mathematische DetailsAuthor: Hans Lohninger
Ein Polynomfilter kann als eine stückweise Anpassung einer Polynomfunktion an das Signal angesehen werden. Die Anpassung wird durch eine Least-Squares-Schätzung (LS-Schätzung) zwischen der Matrix X und dem Vektor y durchgeführt: Die geschätzten Werte, die für die Glättung verwendet werden, sind:  = Xb =
X(XTX)-1XTy =
Hy. = Xb =
X(XTX)-1XTy =
Hy.Das Produkt H =
X(XTX)-1XTy wird
auch die "hat"-Matrix genannt und ist für jedes y für ein gegebenes
Polynom dasselbe. Sie kann also einmal berechnet und für eine spätere Anwendung
gespeichert werden. Das haben Savitzky und Golay für Polynome
verschiedenster Ordnung und Stücke verschiedener Länge n (Originalpublikation in
Anmerkung: Die (n+1)-te Zeile der H-Matrix enthält die tabulierten Koeffizienten für die Savitzky-Golay-Filter. Wir verwenden nur die Abschätzung für den Mittelpunkt des sich bewegenden Fensters für die Glättung. Die anderen Zeilen werden nur für die Glättung des Endpunkts des Signals verwendet, wenn weniger Werte als die Fenstergröße 2n+1 übrig sind. Die Matrix X ist die so genannte Vandermond-Matrix. Wenn wir eine Polynomfunktion der Ordnung p anpassen wollen, bekommen wir eine Reihe von Gleichungen der folgenden Form: yi = bp . xip + bp-1 . xip-1 + ... b1 . xi1 + b0 . xi0 , for i = 1 .. 2n+1. Im Fall, dass n=1, x = [-1 0 +1] erhalten wir:
 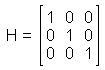 , ,das in den Filterkoeffizienten b = [0 1 0] resultiert. In diesem speziellen Fall würde man eigentlich keine Berechnungen ausführen, sondern nur die Originalwerte heranziehen. Für n = 5 und p = 3 sind die Filterkoeffizienten b = [-0.0857 0.3429 0.4857 0.3429 -0.0857]. Als einen Spezialfall können wir auch den gleitenden Mittelwert ableiten, d.h. wir wollen eine konstante Linie anpassen (ein Polynom nullter Ordnung): 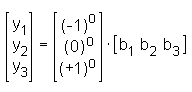 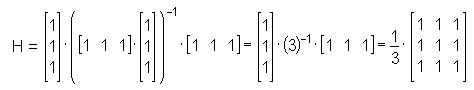
|
|
Home  Bivariate Daten Bivariate Daten  Glättung Glättung  Savitzky-Golay Filter Mathematische Details Savitzky-Golay Filter Mathematische Details |
|
Last Update: 2012-10-08

