Nachweisgrenze

Author: Hans Lohninger

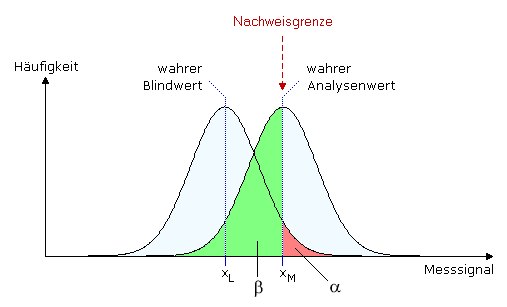
Jedes Messverfahren hat Grenzen bzgl. der kleinsten noch bestimmbaren Substanzmenge. Je weniger Substanz bestimmt wird, desto geringer wird sich der gemessene Wert vom Blindwert unterscheiden. Da aber sowohl der Blindwert als auch der gemessene Wert von Fall zu Fall schwanken (also eine Verteilung aufweisen) wird die richtige Zuordnung des gemessenen Wertes umso unsicherer, je mehr sich der wahre Analysenwert dem wahren Blindwert nähert. Die folgende Abbildung zeigt diese Situation:

Die Nachweisgrenze (engl. limit of detection) ist nun jener Wert, bei dem die Chance, irrtümlich den Blindwert als Nutzsignal zu identifizieren, fünf Prozent ist (α = 0.05). Gleichzeitig bedeutet das aber auch, dass die Hälfte aller Messungen des Nutzsignals als Blindwert qualifiziert wird (β = 0.5), falls der wahre Analysenwert exakt an der Nachweisgrenze liegt. Die Nachweisgrenze hat also für die Erkennung des Vorhandenseins eines Signals wenig Bedeutung, da in der Hälfte der Fälle das Signal irrtümlich als nicht existent qualifiziert wird (man spricht vom Fehler 2. Art). Man sieht also, dass der Fehler 2. Art (repräsentiert durch β) an der Nachweisgrenze unakzeptabel hoch ist. Um den Fehler 2. Art auf ein akzeptables Niveau zu bringen führt man deshalb eine zweite Grenze ein, die Erfassungsgrenze, bei der der Fehler 2. Art auf das selbe Niveau wie der Fehler 1. Art gefallen ist (α = β).

Die exakte Bestimmung der Nachweisgrenze hängt aber nicht nur von der Streuung der Messwerte ab, sondern auch von der Steigung der Kalibrationsgeraden. Details dazu findet man z.B. in Funk et al. . In der Praxis genügt es aber meist in erster Näherung zu verlangen, dass das Nutzsignal um das Doppelte (bei α = 0.05) oder das Dreifache (bei α = 0.01) der Standardabweichung des Untergrundsignals s_u über dem Mittelwert des Blindwerts y_u liegen muss. Damit ergibt sich für die Nachweisgrenze (NWG):

NWG = y_u + 2*s_u (α = 0.05),

bzw.

NWG = y_u + 3*s_u (α = 0.01).

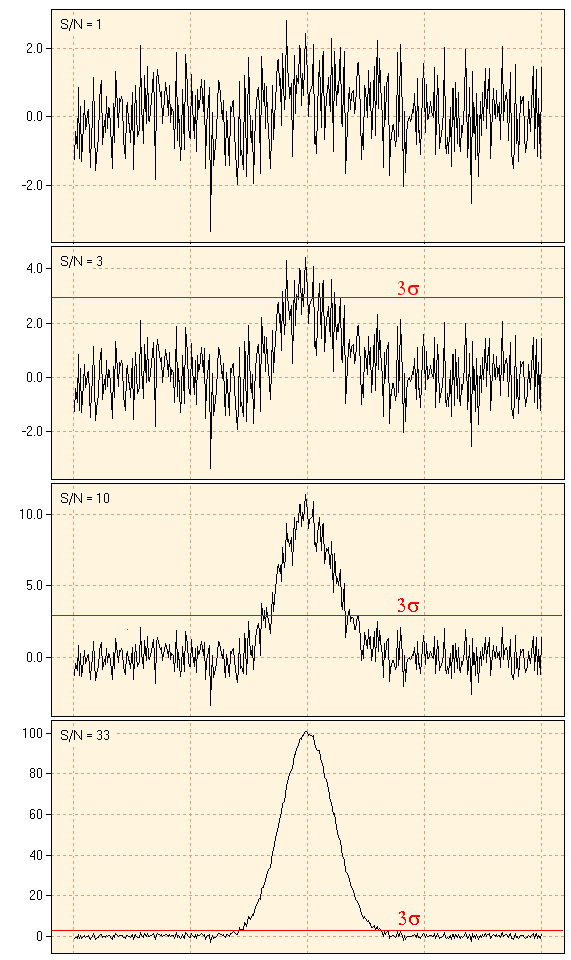
Die folgende Abbildung zeigt einige typische Situationen. Im obersten Bild ist das Nutzsignal etwa so groß wie das Rauschen des Blindwertes. Hier ist das Signal kaum zu erkennen. Im zweiten Diagramm erreicht das Nutzsignal gerade die Nachweisgrenze (Signal/Rausch-Verhältnis = 3). In den beiden unteren Diagrammen liegt das Nutzsignal bei der zehnfachen bzw. 33-fachen Nachweisgrenze.

Beispiele unterschiedlicher Signal/Rausch-Verhältnisse. Erst ab etwa einer Größe von 3 oder höher tritt das Signal klar hervor.