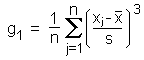Schiefe

Author: Hans Lohninger

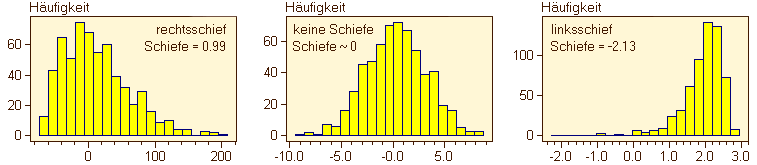
Eine Verteilung wird rechtsschief (bzw. linkssteil) genannt, wenn der Hauptanteil der Verteilung auf der linken Seite konzentriert ist. Für linksschiefe (bzw. rechtssteile) Verteilungen gilt dasselbe für die rechte Seite der Verteilung. Der Grad der Schiefe (engl. skewness) wird durch das dritte Moment der Verteilung bestimmt:

Um zu testen, ob die berechnete Schiefe tatsächlich auf eine schiefe Verteilung schließen lässt, berechnet man folgende Testgröße:

Übersteigt diese das (1-α/2)-Quantil der Standardnormalverteilung, so kann man die Annahme der Symmetrie auf einem Signifikanzniveau von α verwerfen. Für diesen Test sollte n größer als 100 sein.

Hinweis:

In manchen Statistikprogrammen wird die oben berechnete Testgröße Zn als "standardisierte Schiefe" bezeichnet. Als Faustregel gilt, dass mit 95%iger Wahrscheinlichkeit eine schiefe Verteilung vorliegt, wenn die standardisierte Schiefe kleiner als -2 bzw. größer als +2 ist.

Bitte beachten Sie, dass die Schiefe manchmal durch unterschiedliche Formeln definiert wird, was zu veschiedenen Schiefemaßen führt.

Unten finden Sie zwei Beispiele von schiefen Verteilungen. Sie können das folgende interaktive Beispiel starten, um den Effekt von schiefen Verteilungen auf den Mittelwert und den Median zu beobachten.