Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu.

Home Univariate Daten Lagemaße Median
Siehe auch: Mittelwert, Modus einer Verteilung, Quantil, Quartil 
 
Search the VIAS Library  |  Index


Median

Author: Hans Lohninger

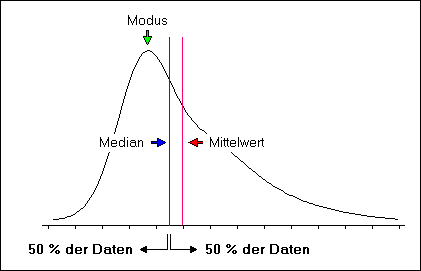
Wenn wir die Verteilungskurve (oder das Histogramm) einer Stichprobe betrachten, so liegt der Median an der Stelle auf der x-Achse, an der die Fläche unter der Kurve (oder die Fläche des Histogramms) exakt in zwei Teile geteilt wird. Die relative Position des Modus, des Medians und des Mittelwerts liefert einen Hinweis auf die Schiefe einer Verteilung:

Der Median wird wie folgt berechnet:

  • Alle Werte werden in aufsteigender Reihenfolge geordnet.
  • Wenn die Anzahl der Werte ungerade ist, wird die mittlere Zahl verwendet.
  • Wenn die Anzahl der Werte gerade ist, wird der Durchschnitt der zwei mittleren Zahlen ausgewählt.
Die Summe der absoluten Abweichungen eines Stichprobenwerts von ihrem Median sind geringer als die absoluten Abweichungen eines beliebigen anderen Werts. Unter bestimmten Umständen kann der Median ein stabileres Lagemaß als der Mittelwert sein. Der Median ist weniger anfällig für Ausreißer (Extremwerte) als der Mittelwert. Die Medianstatistik wird daher oft in Zusammenhang mit der robusten Statistik genannt.

Beispiel: Berechnen Sie den Median folgender Werte: 
4.4; 5.1; 4.1; 6.2; 5.7; 5.6; 7.0
  1. Ordnen Sie die sieben Werte in aufsteigender Reihenfolge: 4.1; 4.4; 5.1; 5.6; 5.7; 6.2; 7.0
  2. Nehmen Sie nun den mittleren Wert (da die Anzahl der Werte ungerade ist) als Median: 5.6

Median/Mittelwert - wann verwende ich was? - Lagemaße und die Grenzgenialität unserer Bildungssysteme.

Home Univariate Daten Lagemaße Median

Last Update: 2012-10-08